3. Trigonometry

f. Applications of Trig Functions

1. Similar and Congruent Triangles

Consider \(2\) triangles:
 \(\triangle ABC\) has angles \(A\), \(B\) and \(C\) and opposite edges \(a\), \(b\) and \(c\).
 \(\triangle DEF\) has angles \(D\), \(E\) and \(F\) and opposite edges \(d\), \(e\) and \(f\).
The \(2\) triangles are called Similar if corresponding angles are equal, i.e. \[ A=D \qquad B=E \qquad C=F \]

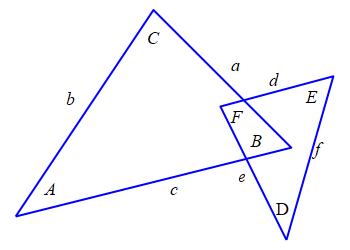
def_sim_tri

If \(2\) triangles \(\triangle ABC\) and \(\triangle DEF\) are similar, then the ratios of corresponding sides are equal: \[ \dfrac{a}{d}=\dfrac{b}{e}=\dfrac{c}{f} \] or equivalently: \[ \dfrac{a}{b}=\dfrac{d}{e} \qquad \dfrac{a}{c}=\dfrac{d}{f} \qquad \dfrac{b}{c}=\dfrac{e}{f} \]

Since the triangles \(\triangle ABC\) and \(\triangle DEF\) are similar, we know \(A=D\) and \(B=E\). By the Law of Sines, applied to sides \(a\) and \(b\) of triangle \(\triangle ABC\) and separately to sides \(d\) and \(e\) of \(\triangle DEF\), we have: \[ \dfrac{a}{b}=\dfrac{\sinA}{\sinB} =\dfrac{\sinD}{\sinE}=\dfrac{d}{e} \] Similarly, we have: \[ \dfrac{a}{c}=\dfrac{d}{f} \qquad \dfrac{b}{c}=\dfrac{e}{f} \] These are the second form of the proposition.
Flipping the fractions in the last two equations gives: \[ \dfrac{a}{d}=\dfrac{c}{f} \qquad \dfrac{b}{e}=\dfrac{c}{f} \] which are the first form of the proposition.

If a \(6\,\text{ft}\) man has a \(2\,\text{ft}\) shadow, how tall is a tree which has an \(8\,\text{ft}\) shadow?

ex_sim_man_tree_shadows

The tree is \(24\,\text{ft}\) tall.

Let \(h\) and \(H\) be the heights of the man and the tree.
Let \(s\) and \(S\) be the lengths of their shadows. Then \[ \dfrac{H}{S}=\dfrac{h}{s} \quad \text{or} \quad H=\dfrac{S}{s}h \] Putting in numbers: \[ H=\dfrac{8}{2}6=24\,\text{ft} \]

Consider \(2\) triangles:
 \(\triangle ABC\) has angles \(A\), \(B\) and \(C\) and opposite edges \(a\), \(b\) and \(c\).
 \(\triangle DEF\) has angles \(D\), \(E\) and \(F\) and opposite edges \(d\), \(e\) and \(f\).
The \(2\) triangles are called Congruent if corresponding sides are equal, i.e. \[ a=d \qquad b=e \qquad c=f \]

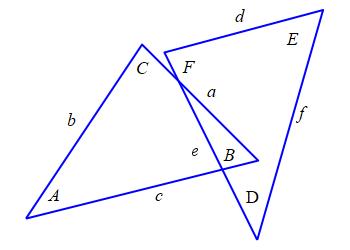
def_cong_tri

If \(2\) triangles \(\triangle ABC\) and \(\triangle DEF\) are congruent, then they are similar. In other words: \[ \text{If}\quad a=d,\ b=e\ \text{and}\ c=f\quad \text{then}\quad A=D,\ B=E\ \text{and}\ C=F \]

Since the triangles \(\triangle ABC\) and \(\triangle DEF\) are congruent, we know \(a=d\), \(b=e\) and \(c=f\). By the Law of Cosines, applied to the angle \(C\) of triangle \(\triangle ABC\) and separately to the angle \(F\) of \(\triangle DEF\), we have: \[ \cos C=\dfrac{c^2-a^2-b^2}{2ab} =\dfrac{f^2-d^2-e^2}{2de}=\cos F \] So \(C=F\). Similarly, \(A=D\) and \(B=E\).

An isosceles triangle is a triangle with two sides equal. In the triangle \(\triangle ABC\), assume \(a=b\).
Prove the median from \(C\) to the midpoint, \(M\), of the opposite side, \(AB\), also bisects the angle \(C\), i.e. \(\alpha=\beta\).
Further, prove the other two angles are equal, i.e. \(A=B\).

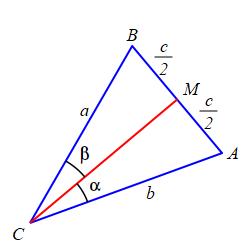
ex_sim_pf_med_bisect

Let \(m\) be the length of the median, \(CM\).
Then triangle \(\triangle CAM\) has sides \(b\), \(\dfrac{c}{2}\) and \(m\) and triangle \(\triangle CBM\) has sides \(a\), \(\dfrac{c}{2}\) and \(m\).
But \(a=b\). They are congruent! So corresponding angles are equal: \[ \alpha=\beta \quad \text{and} \quad A=B \]

© MYMathApps

Supported in part by NSF Grant #1123255